Loi de Pareto - Math'φsics

Loi de Pareto

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Loi de Pareto de paramèrtes \(r,\alpha\)
Loi caractérisée par : $${\Bbb P}(X\gt x)=\left(\frac rx\right)^\alpha\quad\text{ avec }\quad x\geqslant r$$
- densité : \(f_{r,\alpha}(x)=\) \(\alpha\frac{r^k}{x^{k+1} }\)
Exercices

La loi de Pareto admet comme fonction de répartition : $$F_\theta:x\mapsto(1-(r/x)^\alpha)\Bbb 1_{x\geqslant r}.$$Montrer que les lois de Pareto sont absolument continues par rapport à la mesure de Lebesgue et calculer la densité \(f_{r,\alpha}\).

Pour avoir la densité, il suffit de dériver la fonction caractéristique (via Théorème fondamental d'analyse).

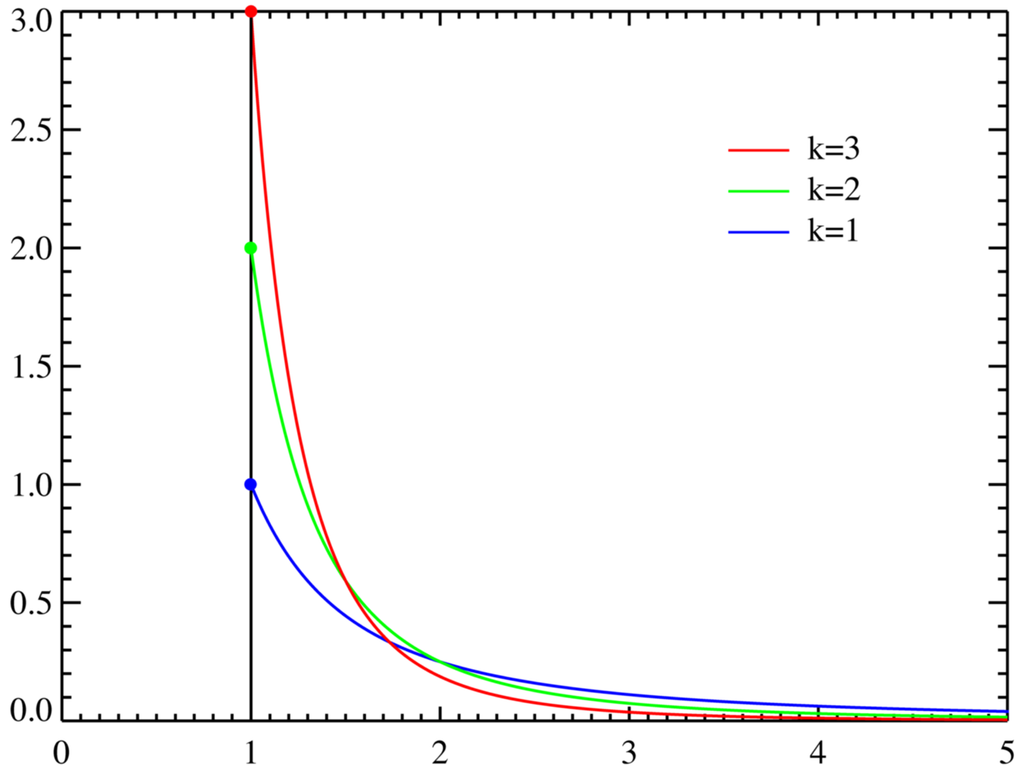
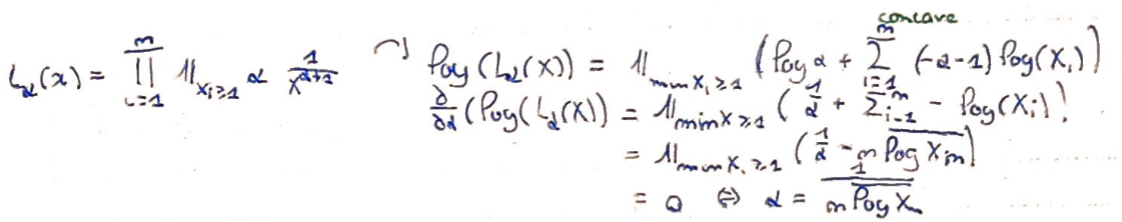On considère la loi de Pareto, de densité : $$f_{r,\alpha}(x)=\alpha\frac{r^k}{x^{k+1} }.$$On suppose que \(r\) est connu et vaut \(1\). Calculer l'estimateur du maximum de vraisemblance \(\hat\alpha_n\) de \(\alpha\).

On passe au \(\log\) et on dérive.
Rétroliens :
- Densité de probabilité